通俗理解卡尔曼滤波

1.核心思想

问题的引出

我们想要知道某个时刻汽车到了哪个位置（比如经纬度或者汽车走了多少路程），如图所示，怎么做到呢？

方法一：我们可以通过GPS获取位置信息来判断，但是民用的GPS精度大约为10米，这个误差还是比较大的（我们可能离终点十米就被GPS判定到达了终点，也有可能超过终点十米）。

方法二：我们可以通过历史信息，比如通过前一个时刻汽车的位置、速度、加速度等信息来推断当前时刻的汽车位置，也就是通过建立模型来推测位置信息。但是速度加速度等仪器也有误差，而且还有环境因素比如风的影响，仅仅靠物理模型会形成累积误差，越错越多。

解决方法

卡尔曼的方法本质上是结合这两种方法，也就是对两个方法取一个加权平均，用这个值作为估计值。比如GPS说汽车行驶了85米，用物理模型推出汽车行驶了80米，如果说GPS的准确率是90%，物理模型准确率是80%，那么汽车行驶的距离为：

距离$=\left(1-\frac{0.9}{0.8+0.9}\right) * 80+\frac{0.9}{0.8+0.9} * 85=82.65米$

这就是卡尔曼滤波的核心思想了，如果想进一步了解公式大体含义，可以看下去。少侠请留步，能否点个赞鼓励一下？

2.过程及公式的大体理解

这里我不想一步一步去将公式推导出来，那样就显得太繁琐了，我只是尽可能将每一个公式的含义做一个通俗的理解。

卡尔曼滤波的假设条件

线性系统：我理解的线性系统就是公式仅有多项式，而非线性系统就是含有cosx这种值。（这里查过一些资料，但是说的都太学术化，没有很好理解，欢迎各位大佬指正）扩展卡尔曼滤波就是将这些非线性的公式用一阶泰勒展开，转换成线性方程再用卡尔曼滤波求解。

状态方程

这里的公式就是我们前面说的通过历史信息建立物理模型得到的，x(t)就是t时刻状态向量，包含t时刻的位置、速度等状态信息，它等于一个时刻x(t-1)状态向量的A变换（当然我们求距离的话这里A就是[1]了），加上t
时刻控制变量u(t)，比如加速度就是控制变量，加上外界环境的影响比如风，我们将其视为服从正态分布的过程噪声w(t)，均值为0方差为Q，这就是一个完整的状态方程了。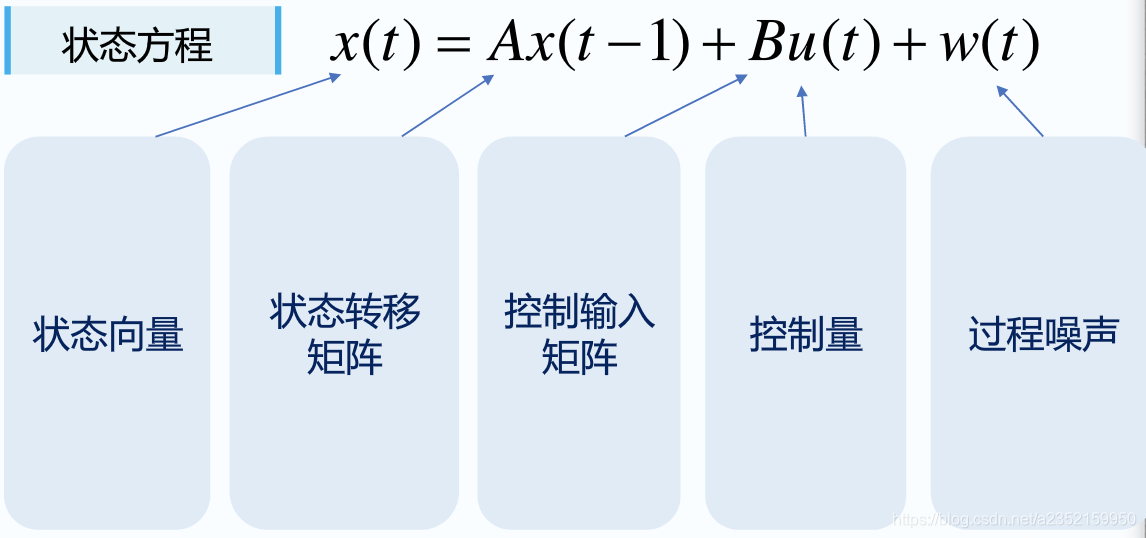

观测方程

z(t)就是我们说的仪器观测值（比如GPS读数），他可以通过观测矩阵乘上状态矩阵（这里的观测矩阵就是通过仪器来获取的，表明从状态矩阵到观测矩阵的一个映射），后面的v(t)就是观测噪声，表明仪器的观测误差，均值为0，方差为R。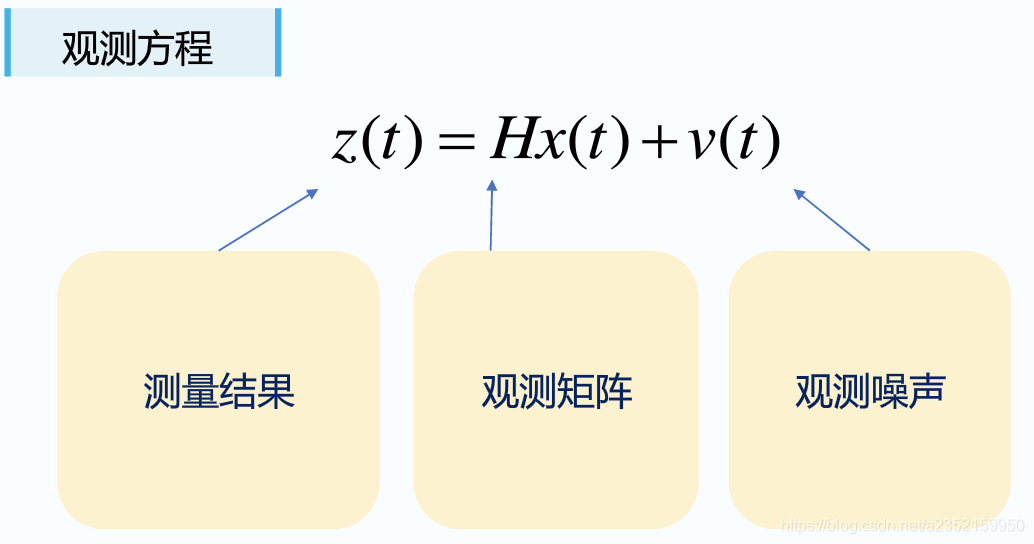

协方差矩阵？为啥要引入？

这里我不得不吐槽一下网上的“通俗理解”博客，很多都是一带而过，写写公式就完事了，其实这里很重要好吧。

卡尔曼认为位置、速度这些状态信息都服从正态分布，比如我们前面提到的例子，下图黄色的曲线就是基于历史信息物理模型的分布函数，在80米处的准确率最大为80%，灰色曲线就是GPS观测值分布函数，在85米的位置准确率最大为90%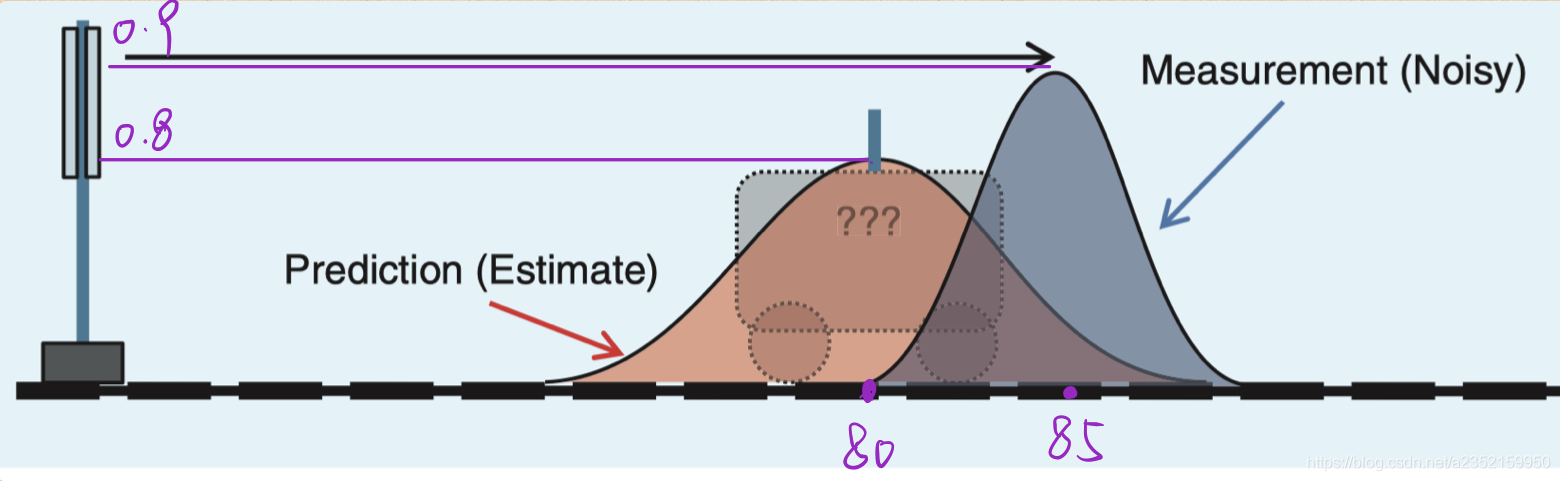
卡尔曼认为两个正态分布函数相交的地方就是汽车最有可能在的位置。如何得到这个绿色的区域函数呢，当然就要先求出黄色和灰色的正态分布函数了。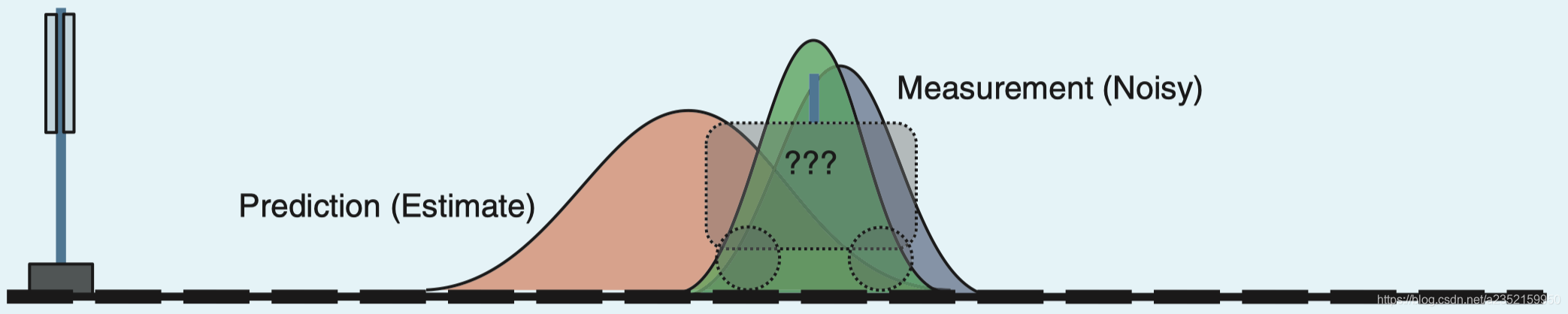

下面的图片来自wiki

一维正态分布的函数如下，是以均值和方差的形式写出来的

然而状态方程并不是一维的，而是由很多决定因素（位置、速度等），因此要引入多元正态分布，公式如下（别怕，公式就瞄一眼就好了），一看就明白了，原来计算协方差是为了计算多元正态分布函数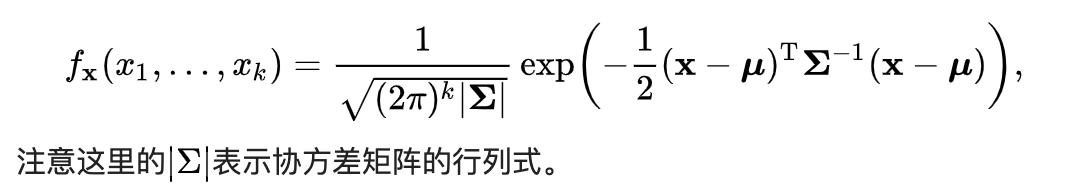

下面的公式就是计算状态量和协方差矩阵，这里面的数学推导有兴趣的同学可以去看看，网上这个推导还是很多的

计算最优估计值

我们上面说的计算两个正态函数相交的绿色区域，其实就是一个加权平均的体现，就是我们一开始说的例子。这个加权平均值在卡尔曼滤波中被称为误差增益，如下图所示，它的加权平均值计算推导可以参考下面的论文（有兴趣的同学可以看一下）：

然后我们将当前时刻的最优估计值重新赋值给上一时刻的位置信息，这样就形成了一个循环，不停地优化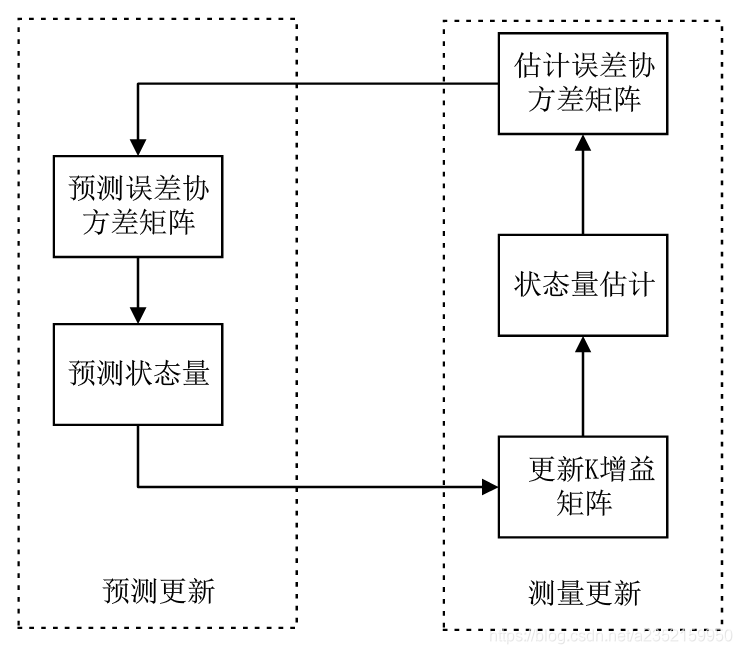

终于讲完了，我没有对数学公式进行过多的讲解，毕竟我们只是需要理解核心思想，公式推导什么的交给数学家去做吧，希望有收获的同学点个赞，让更多的人看到，也欢迎大家对本文进行批评指正。